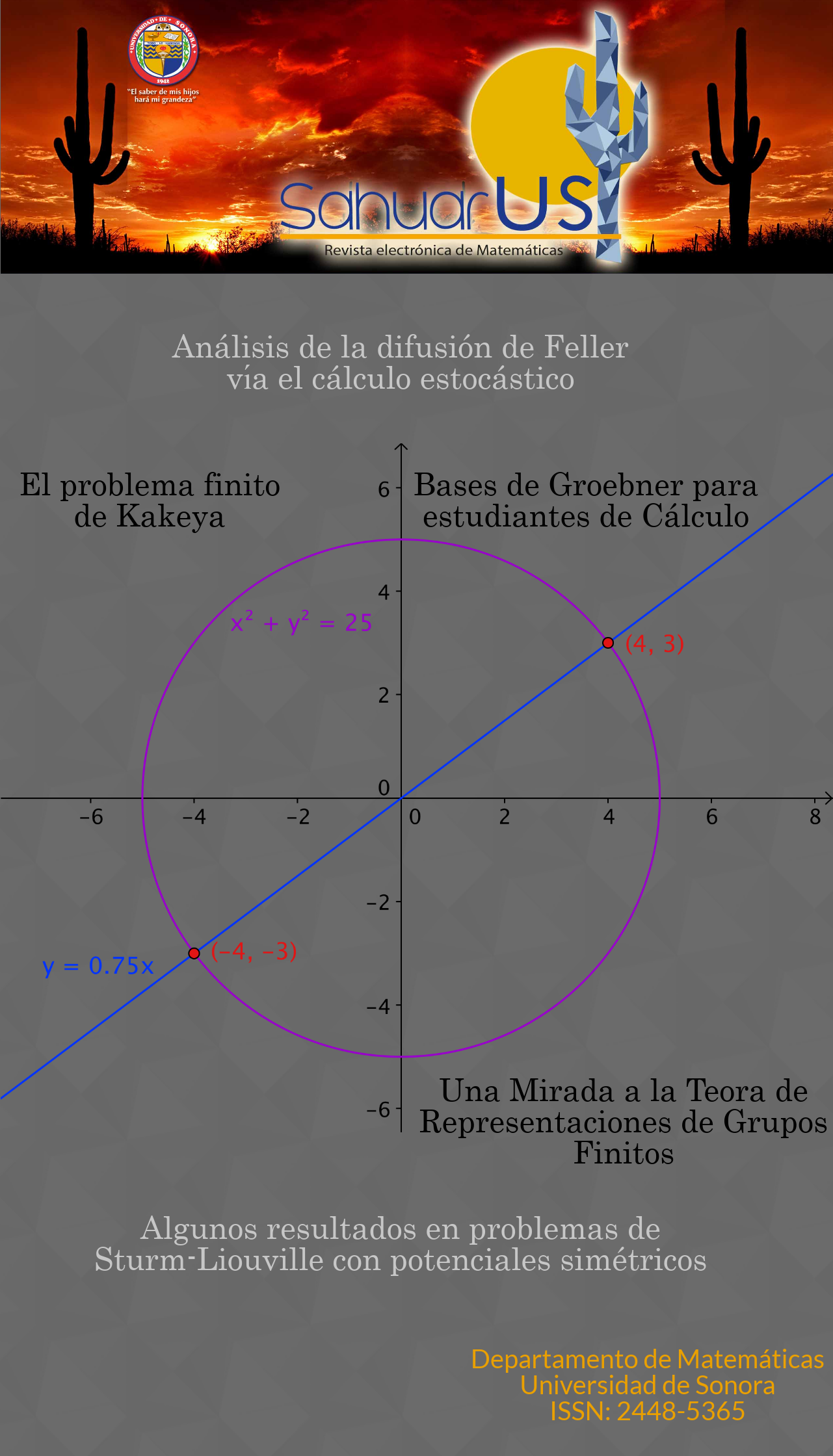
El problema finito de Kakeya
DOI:
https://doi.org/10.36788/sah.v3i1.93Resumen
En este trabajo se presenta la notable solución de Zeev Dvir al problema finito de Kakeya. Este es un problema en la frontera entre combinatoria y análisis armónico. Por mucho tiempo se consideró un problema muy difícil por los expertos en el área, pero la prueba de Dvir tiene apenas dos páginas de largo y apenas requiere algunos conceptos básicos (nociones elementales de álgebra lineal y polinomios) para su exposición.
Descargas
Citas
Aigner, M. and Ziegler, G.M., Proofs from the Book, 5th. Edition, Springer-Verlag Berlin Heidelberg, (2014). DOI: https://doi.org/10.1007/978-3-662-44205-0
Besicovitch, A. S., On Kakeya’s problem and a similar one, Mathematische Zeitschrift,Vol. 27, no. 1, pp. 312-320, (1928). DOI: https://doi.org/10.1007/BF01171101
Bourgain, J., Katz, N. and Tao, T., A sum-product estimate in finite fields, and applications, Geometric and Functional Analysis, Vol. 14, no. 1, pp.27-57, (2004). DOI: https://doi.org/10.1007/s00039-004-0451-1
Bourgain, J., Harmonic analysis and combinatorics: how much may they contribute toeach other, Mathematics: Frontiers and Perspectives (V. Arnold. et al., eds.), pp. 13-32,(2000).
Davies, R. O., Some remarks on the Kakeya problem, Mathematical Proceedings of the Cambridge Philosophical Society, Vol. 69, no. 3, pp. 417-421, (1971). DOI: https://doi.org/10.1017/S0305004100046867
DeMillo, R. A., and Lipton, R. J., A probabilistic remark on algebraic program testing, Information Processing Letters Vol. 7, no. 4, pp. 193-195, (1978). DOI: https://doi.org/10.1016/0020-0190(78)90067-4
Dvir, Z., Incidence theorems and their applications, Foundations and Trends in The oretical Computer Science, Vol. 6, no.4, pp. 257-393, (2012). DOI: https://doi.org/10.1561/0400000056
Dvir, Z., On the size of Kakeya sets in finite fields, Journal of the American Mathematical Society Vol. 22, no. 4, pp. 1093-1097, (2009). DOI: https://doi.org/10.1090/S0894-0347-08-00607-3
Falconer, K. J., The geometry of fractal sets, Vol. 85. Cambridge university press,(1986). DOI: https://doi.org/10.1017/CBO9780511623738
Fujiwara, M. and Kakeya, S., On some problems of maxima and minima for the curveof constant breadth and the in-revolvable curve of the equilateral triangle, TohokuMathematical Journal, Vol. 11, pp. 92-110, (1917).
Guth, L., Polynomial methods in combinatorics, Vol. 64, American Mathematical Soc.(2016). DOI: https://doi.org/10.1090/ulect/064
Jukna, S., Extremal combinatorics: with applications in computer science, 2nd. Edition,Springer-Verlag Berlin Heidelberg, (2011). DOI: https://doi.org/10.1007/978-3-642-17364-6
Kakeya, S., Some problems on maxima and minima regarding ovals, Tohoku ScienceReports, Vol. 6, pp. 71-88, (1917).
Katz, N. H., and Tao., T. Bounds on arithmetic projections, and applications to the Kakeya conjecture, Mathematical Research Letters, Vol. 6, no. 5-6, pp. 625-630, (1999). DOI: https://doi.org/10.4310/MRL.1999.v6.n6.a3
López Ruiz, Jonathan, A 100 años del problema de Kakeya: origen y perspectivas, Tesis de licenciatura, Universidad Nacional Autónoma de México, 2017.
Mattila, P., Fourier analysis and Hausdorff dimension, Vol. 150, Cambridge UniversityPress, (2015). DOI: https://doi.org/10.1017/CBO9781316227619
Mockenhaupt, G. and Tao, T., Restriction and Kakeya phenomena for finite fields, DukeMathematical Journal, Vol. 121, no. 1, pp. 35-74, (2004). DOI: https://doi.org/10.1215/S0012-7094-04-12112-8
Moshkovitz, D., An Alternative Proof of The Schwartz-Zippel Lemma, Electronic Colloquium on Computational Complexity (ECCC), Vol. 17. no. 96, p. 34, (2010).
Pál, J., Ein minimumproblem für Ovale, Mathematische Annalen, Vol. 83, no. 3, pp.311-319, (1921). DOI: https://doi.org/10.1007/BF01458387
Rogers, K. M., The finite field Kakeya problem, The American Mathematical Monthly,Vol. 108, no. 8, pp. 756-759, (2001). DOI: https://doi.org/10.1080/00029890.2001.11919808
Schwartz, J. T., Fast probabilistic algorithms for verification of polynomial identities,Journal of the ACM (JACM) Vol. 27, no. 4, pp. 701-717, (1980). DOI: https://doi.org/10.1145/322217.322225
Stein, E. M. and Shakarchi, R., Real analysis: measure theory, integration, and Hilbertspaces, Princeton University Press, (2009). DOI: https://doi.org/10.2307/j.ctvd58v18
Tao, T., Algebraic combinatorial geometry: the polynomial method in arithmetic combinatorics, incidence combinatorics, and number theory, arXiv preprint arXiv:1310.6482 https://arxiv.org/abs/1310.6482 ( 2013). Accessed 16 October 2017.
Tao, T., A new bound for finite field Besicovitch sets in four dimensions, Pacific journalof mathematics, Vol. 222, no. 2, pp. 337-363, (2005). DOI: https://doi.org/10.2140/pjm.2005.222.337
Tao, T., From Rotating Needles to Stability of Waves: Emerging connections between combinatorics, analysis and PDE, Notices of the AMS, Vol. 48, no 3, pp. 294-303, (2001).
Tao, T., Poincaré’s Legacies, Part II: pages from year two of a mathematical blog, American Mathematical Soc., (2009). DOI: https://doi.org/10.1090/mbk/067
Wolff, T., Recent work connected with the Kakeya problem. Prospects in mathematics(Princeton, NJ, 1996), Vol. 2, pp. 129-162, (1999).
Zippel, R., Probabilistic algorithms for sparse polynomials, Ng E.W. (eds) Symbolicand Algebraic Computation. EUROSAM. Lecture Notes in Computer Science, Vol. 72, Springer, Berlin, Heidelberg, pp. 216-226, (1979). DOI: https://doi.org/10.1007/3-540-09519-5_73
Descargas
Publicado
Cómo citar
Número
Sección
Licencia
Los artículos publicados por Sahuarus. Revista Electrónica de Matemáticas se distribuye bajo una Licencia Creative Commons Atribución-NoComercial-SinDerivadas 4.0 Internacional, la cual permite la distribución y el uso del material publicado citando la fuente de la que proviene, prohibe la modificación y el uso con fines comerciales.